Der folgende Text hat sechs Abschnitte. Ordnen Sie den Abschnitten die passenden Abbildungen zu.
Zahnrad,
Maschinenelement zur Übertragung von Drehbewegungen bzw. Drehmomenten zwischen zwei Wellen bei geringem Wellenabstand; es besteht aus einer kreisförmigen Scheibe mit Verzahnungen am Rand.
Von der Lage der beiden Wellen, zwischen denen eine Bewegungsübertragung erfolgen soll, hängt die Grundform der verwendeten Zahnräder ab. So benutzt man z. B. für¸ parallel laufende Wellen Stirnräder, deren Grundform zylindrisch ist. Am häufigsten werden dabei Räder mit Geradverzahnung benutzt. Schrägverzahnte Räder besitzen eine relativ große Laufruhe, erzeugen jedoch in Längsrichtung der Wellen einen Schub. Bei Pfeilzähnen hebt sich der axiale Schub auf. Kegelräder werden für Wellen, deren Mittellinien sich schneiden, verwendet, Schrauben- und Schneckenräder bei sich kreuzenden Wellen.
Der gleichförmige Lauf der Zahnräder ist vor allem von der Form der seitlichen Begrenzung des Zahnes abhängig. Das häufigste Zahnprofil hat die Form einer Kreisevolvente.
In den meisten Fällen werden Zahnräder durch spanabhebende Bearbeitung, seltener spanlos, durch Gießen, hergestellt.
VerzahnungZwei miteinander kämmende Zahnflanken haben im Berührungspunkt A die gemeinsame Tangente TT und die gemeinsame Normale (Senkrechte) NN. Man nennt den Punkt C, der auf der Verbindungslinie der beiden Radmittelpunkte 0
1,0
2 und auf der Normalen NN im Berührungspunkt der Zahnflanken liegt, den
Wälzpunkt. Gleichförmiges Übersetzungsverhältnis ist nur dann gewährleistet, wenn in jeder beliebigen Zahneingriffsstellung die Senkrechte im jeweiligen und in jedem möglichen Berührungspunkt bei den kämmenden Zahnflanken durch diesen Wälzpunkt geht. Die Kreise mit den Radien r
o1 und r
o2 nennt man die
Wälzkreise. Sie werden als Teilkreise für die Herstellung benutzt. Der auf diesem Kreis gemessene Abstand der Links- oder Rechtsflanken zweier aufeinander folgender Zähne ist die sogenannte
Teilung t. Sie ergibt sich aus dem Teilkreisumfang, dividiert durch die
Zähnezahl z (t = d
0 · π / z).
Der
Modul m ergibt sich auch aus Teilkreisdurchmesser d
0, dividiert durch die Zähnezahl z (m = d
0/z). Die Teilung t ist mit dem Modul m durch die Zahl π verknüpft (t = m · π) . So hat beispielsweise ein Zahnrad mit 37 Zähnen und dem Modul 5 einen Teilkreisdurchmesser von 37 · 5 = 185 mm und eine Zahnteilung t = 5 · π = 5 · 3,14 = 15,70 mm. Verbindet man sämtliche möglichen Berührungspunkte, der Flanken einer Radpaarung miteinander, so erhält man die sogenannte
Eingriffslinie. Damit Räder zusammenarbeiten können, müssen sie erstens gleiche Teilung besitzen, zweitens mindestens ein Zahnpaar im Eingriff haben und drittens außerdem übereinstimmende und sich deckende Eingriffslinien aufweisen. Räder, die diese drei Bedingungen erfüllen, bilden einen Rädersatz, sie können wahllos miteinander gepaart werden.
Ordnen Sie die Abbildungen den entsprechenden Abschnitten zu!
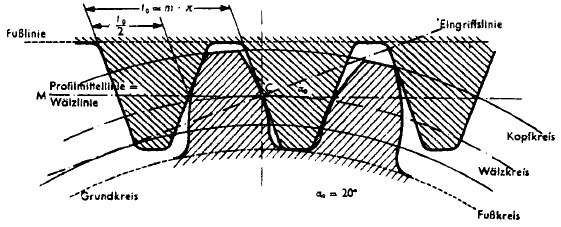
Abbildung 1 gehört zu Abschnitt
.
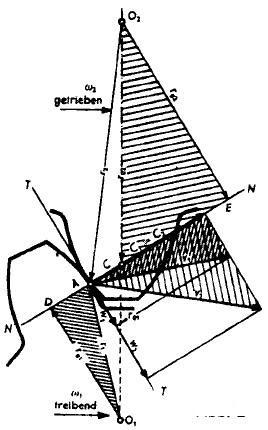
Abbildung 2 gehört zu Abschnitt
.
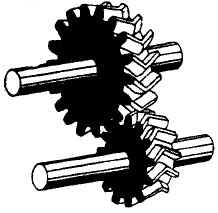
Abbildung 3 gehört zu Abschnitt
.
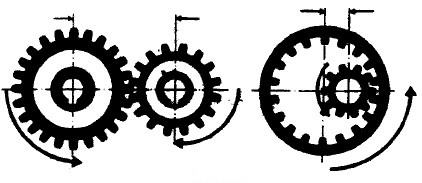
Abbildung 4 gehört zu Abschnitt
bzw.
.
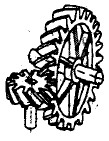
Abbildung 5 gehört zu Abschnitt
.
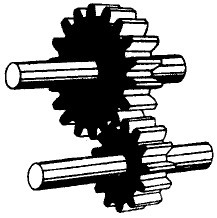
Abbildung 6 gehört zu Abschnitt
.
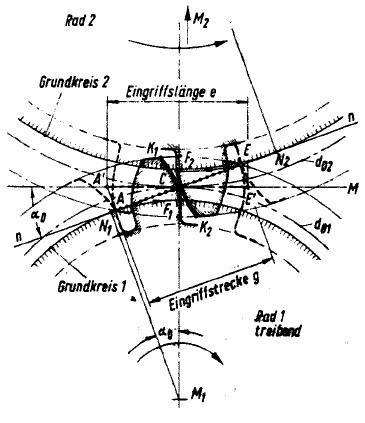
Abbildung 7 gehört zu Abschnitt
.
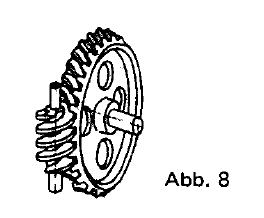
Abbildung 8 gehört zu Abschnitt
.
Abbildung 9 gehört zu Abschnitt
.
Abbildung 10 gehört zu Abschnitt
.